面向模擬智能的計算系統
中國網/中國發展門戶網訊 人類進入大科學時代后,“模擬”作為“理論”“實驗”以外重要的補充技術手段,成為科學研究的第3個支柱。從表現形式看,科學研究可以被視為建立模型(modeling)的過程。而模擬(simulation)則是所建立的科學模型在計算機上的運行過程。最早期的計算機模擬(computer simulation)可以追溯到第二次世界大戰之后,是專門針對核物理學和氣象學研究的一種開創性的科學工具。后來,在越來越多的學科中,計算機模擬變得愈發重要,并不斷衍生出計算和其他領域交叉的學科,如:計算物理、計算化學和計算生物學等學科。Weaver在1948年撰文指出:人類解決有序復雜問題并實現科學新飛躍,將主要依賴于計算機技術的發展和不同學科背景科學家的技術碰撞。一方面,計算機技術的發展使人類能夠解決復雜且難以處理的問題。另一方面,計算機技術能夠有效激發有序復雜性問題的新解決方法。這種新解決方法本身也正是計算科學(computational science)的范疇之一,讓科學家有機會集中資源,將不同領域的見解聚焦在共同問題上。這種見解聚焦的結果,促使不同學科背景的科學家們,形成比單一學科背景科學家們更強大的“混合團隊”;這樣的“混合團隊”將有能力解決某些復雜性問題,并且得出有用的結論。總之,科學和建模緊密相關,模擬執行代表理論的模型,人們把科學研究中的計算機模擬稱為科學模擬(scientific simulation)。
目前,還沒有任何針對“計算機模擬”的單一定義能夠恰當地描述科學模擬的概念。美國國防部將模擬定義為一種方法,即:“一種隨時間實現模型的方法”;進而,將計算機模擬定義為一種過程,即:“在計算機上執行代碼、控制和顯示接口硬件,并與現實世界設備進行接口交互的過程”。Winsberg把計算機模擬的定義又分為狹義和廣義范圍。
在狹義定義中,計算機模擬就是“在計算機上運行程序的過程”。計算機模擬使用步進方法來探索數學模型的近似行為。模擬程序在計算機上的一次運行過程,代表了對目標系統的一次模擬。人們愿意用計算機模擬方法求解問題,主要有以下2個原因:原始模型本身包含離散方程;原始模型的演化更適合用“規則”,而不是“方程”來進行描述。值得注意的是,這種狹義角度指代計算機模擬時,需要限定到特定處理器硬件上算法的實現、用特定編程語言編寫應用,以及核函數程序、使用特定編譯器等限制條件。在不同應用問題的場景下,由于這些限制條件的變化,通常會獲得不同的性能結果。
在廣義定義中,可以把計算機模擬看作研究系統的一種綜合方法,是更加完整的計算過程。該過程包括模型選擇、通過模型實現、算法輸出計算、結果數據可視化及研究。整個模擬的過程也可以與科學研究過程進行對應,如Lynch所描述:提出一個經驗上可回答的問題;從旨在回答該問題的理論中推導出一個可證偽的假設;收集(或發現)和分析經驗數據以檢驗該假設;拒絕或未能拒絕該假設;將分析結果與得出該問題的理論聯系起來。在過去,這種廣義的計算機模擬通常出現在認識論或者方法論的理論場景中。
Winsberg進一步將計算機模擬劃分為基于方程的模擬(equation-based simulation)和基于主體的模擬(agent-based simulation)。基于方程的模擬常用于物理等理論學科中。這些學科中一般存在主導性的理論,這些理論可以用來指導構建基于微分方程的數學模型。例如,基于方程的模擬可以是針對粒子的模擬,這種模擬通常包含數量巨大的多個獨立粒子和一組描述粒子之間相互作用的微分方程。此外,基于方程的模擬也可以是基于場的模擬,通常包含一組描述連續介質或場的時間演化方程。基于主體的模擬往往遵循某種演化規則,是模擬社會和行為科學的最常見方式。例如, Schelling的隔離政策模型。盡管基于主體的模擬在一定程度上可以表示多個主體的行為,但與基于方程的粒子模擬不同,這里沒有控制粒子運動的全局微分方程。
從計算機模擬的定義和分類中,可以看出人們對科學模擬不同層次的期望。從狹義的計算機模擬角度看,它已經成為理論分析和實驗觀察等傳統認知方式的補充手段。科學或工程領域無一例外是由計算機模擬推動的,在某些特定應用領域和場景下,甚至是由計算機模擬改變的。如果沒有計算機模擬,許多關鍵技術就無法被理解、開發和利用。廣義的計算機模擬蘊含著一個哲學問題:計算機是否可以自主進行科學研究?科學研究的目標是認識世界,這意味著計算機程序必須創造新的知識。隨著人工智能技術研究及應用的新一輪爆發,人們對計算機自動地以“智能”方式進行科學研究充滿了期待。值得一提的是,Kitano在2021年提出的“諾貝爾-圖靈挑戰”的新觀點——“到2050年,開發能夠自主執行研究任務的智能科學家,做出諾貝爾獎級別的重大科學發現”。該觀點涉及狹義和廣義的計算機模擬相關技術,但沒有圍繞廣義定義的“哲學問題”深入探討,只是把其作為科學模擬的一個宏偉目標看待。
科學模擬的發展階段
從最直觀的視角來看,科學模擬的載體是計算機程序。從數學形式上講,計算機程序是由可計算函數組成的,其中每個函數將有限輸入數據的離散集映射到有限輸出數據的離散集上。從計算機技術上講,計算機程序等于算法加上數據結構。因此,科學模擬的實現需要以科學問題及其解決方式被形式化抽象為條件。這里,本文借用Simon的觀點:科學家即問題“求解器”。在此觀點中,科學家給自己設定了重大科學問題,確定問題和解決問題的策略和技術是科學發現的本質。基于上述“求解器”的話語體系,本文類比求解方程的形式,將科學模擬的發展劃分為3個階段,即數值計算、模擬智能和科學大腦(圖1)。
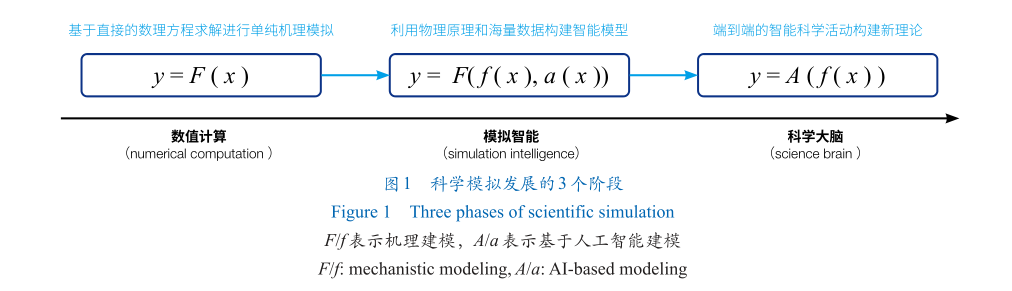
數值計算
然而,這種將部分復雜科學問題轉換為相對簡單的計算問題的解題模式,僅僅是一種粗粒度的建模方案,在一些應用場景下會遇到計算瓶頸。在解決真實場景中復雜物理模型時,常常面臨基本物理原理計算量過大的問題,并由此導致空有原理而無法有效解決科學問題。例如,第一性原理分子動力學的關鍵為求解量子力學Kohn-Sham方程,其核心算法求解過程是多次求解大規模特征值問題。特征值問題的計算復雜度為N3(N為矩陣的維度)。在實際物理問題的求解中,最常用的平面波基組通常是原子個數的100—10000倍。這意味著對于上千原子的體系規模,矩陣維度N達到106,其相應的浮點數運算總量也將達到1018 FLOPS,即達到EFLOPS級別的計算量。需要注意的是,在單步分子動力學中需要多次求解特征值問題,這也就使得單步分子動力學的模擬時間通常為數分鐘乃至1小時。由于單步分子動力學的模擬物理時間只能達到1飛秒,假設要完成納秒物理時間的分子動力學模擬過程,就需要106個分子動力學步。相應的計算量至少要達到1024 FLOPS。如此龐大的運算量即使使用世界上最大規模的超級計算機也難以在短時間內完成。為了解決僅使用第一性原理計算帶來的超大計算量,研究人員發展了多尺度方法,其中最典型的是獲得了2013年諾貝爾化學獎的量子力學/分子力學(QM/MM)方法。該方法的思想是針對核心物理化學反應部分(如:酶及其結合底物的活躍位點原子),采用高精度的第一性原理計算方法,對于周圍的物理化學反應區域(溶液、蛋白質和其他區域)采用低精度且計算復雜度更低的經典力學方法。這種高精度、低精度相結合的計算方法,可以有效地降低計算量。但面對實際問題時,該方法依然存在著巨大的挑戰。例如,細胞半徑約0.2微米的單個生殖支原體包含3×109個原子和77000個蛋白質分子。由于核心計算時間仍來自QM部分,模擬2小時的過程預計需要耗費109年。如果將類似問題推廣到人腦的模擬中,相應的系統原子數將達到1026個,保守估計需要1010個活躍位點的QM計算。由此可以推斷,模擬1小時的QM部分需要長達1024年的時間,而MM部分的模擬也需要長達1023年的時間。這種超長計算時間的情況也被稱為“維度災難”。
模擬智能
因此,模擬智能在傳統數值計算中嵌入人工智能模型(當前主要是深度學習模型),不同于其他人工智能應用領域的深度學習模型“黑盒子”。模擬智能要求這些模型的基本出發點和基本結構是可解釋的。目前,這一方向已存在大量研究,Zhang等在2023年對模擬智能領域最新進展進行了系統性的梳理。從理解亞原子(波函數和電子密度)、原子(分子、蛋白質、材料和相互作用)到宏觀(流體、氣候和地下)尺度物理世界,把研究對象分為量子(quantum)、原子(atomistic)和連續介質(continuum)三大體系,涵蓋量子力學、密度泛函、小分子、蛋白質、材料科學、分子間相互作用和連續力學等7個科學領域。此外,還詳細討論了其中關鍵的共同挑戰,即:如何通過深度學習方法捕捉物理第一性原理,特別是自然系統中的對稱性。利用物理原理的智能模型幾乎已經滲透了傳統科學計算的所有領域。模擬智能大幅提升了對微觀多尺度系統的模擬能力,為在線實驗反饋迭代提供了更加全面的支撐條件。例如,計算模擬系統和機器人科學家之間的快速實時迭代,有助于提升科研效率。因此,模擬智能在一定程度上,還將包括“理論—實驗”迭代的控制過程,同時也會涉及部分廣義的科學模擬。
科學大腦
傳統的科學方法從根本上塑造了人類探索自然和科學發現的分步“指南”。面對全新的研究問題,科學家們已經被訓練成從假設和替代方案的角度出發,指定如何開展控制測試的定勢思維。雖然這種研究過程在過去幾個世紀內都是有效的,但是非常緩慢的。從某種意義上來說,這種研究過程是主觀的,是由科學家的聰明才智和偏見驅動的。這種偏見,有時會阻礙必要的范式轉變。人工智能技術的發展激發了人們對科學和智能融合產生最優的且具有創新性的解決方案的期望。
以上所提到的科學模擬發展經歷的3個階段,能夠明顯區分計算機模擬在可計算和智能化能力方面逐步提升的過程。數值計算階段,對復雜科學問題中相對簡單的計算問題進行了粗粒度建模,屬于單純的狹義計算機模擬定義范疇。它不僅促進眾多領域宏觀尺度科學發現,同時也開啟了對微觀世界的初步探索。模擬智能階段,將針對微觀世界的多尺度探索推上一個新的臺階。除了在狹義計算機模擬定義范疇內對計算能力進行了數量級地提升之外,該階段還涉及對實驗中某些關鍵環節的計算加速,在一定程度上為科學模擬下一階段的實現奠定了基礎。科學大腦階段,將是對廣義計算機模擬定義的實現。在此階段中,計算機模擬將具備創造知識的能力。
設計模擬智能計算系統的關鍵問題
按照本文對科學模擬發展階段的粗粒度劃分,與其相應的計算系統也在同步進化。超級計算機在數值計算階段發揮了不可替代的作用;發展到新的模擬智能階段,底層計算系統的設計也是基石。那么,模擬智能計算系統的發展方向應該遵循什么樣的指導思想?
縱觀計算和科學研究發展歷史,可歸納出計算系統發展的基本周期性規律:在新的計算模式和需求產生階段的初期,計算系統的設計側重追求極致的專用性。而在經過一段時間的技術演變和應用拓展之后,計算系統的設計開始側重于對通用性的追求。在人類科技文明早期發展的漫長過程中,計算系統曾經是各式各樣的專用機械設備,輔助進行一些簡單的運算(圖2)。近代以來,電子技術的突破催生了電子計算機的出現,并且隨著其計算能力的不斷提升,數學、物理等學科的發展也不斷向前,尤其是超級計算機上的大規模數值模擬成果,引領了大量前沿科學研究和重大工程應用。由此可見,日益發展的通用高性能計算機在不斷地加速宏觀尺度科學的各類大規模應用,并取得重大成果。接下來,微觀世界的多尺度探索將是未來Z級(1021)超級計算機應用的核心場景。而現有通用高性能計算機的技術路線則將遇到功耗和效率等瓶頸,難以為繼。結合模擬智能階段所呈現的新特征,本文認為面向模擬智能的計算系統,將以追求極致的Z級計算專用智能系統為設計目標,未來性能最高的計算系統將專門針對模擬智能應用程序,在硬件本身及軟件底層的算法和抽象中進行定制。
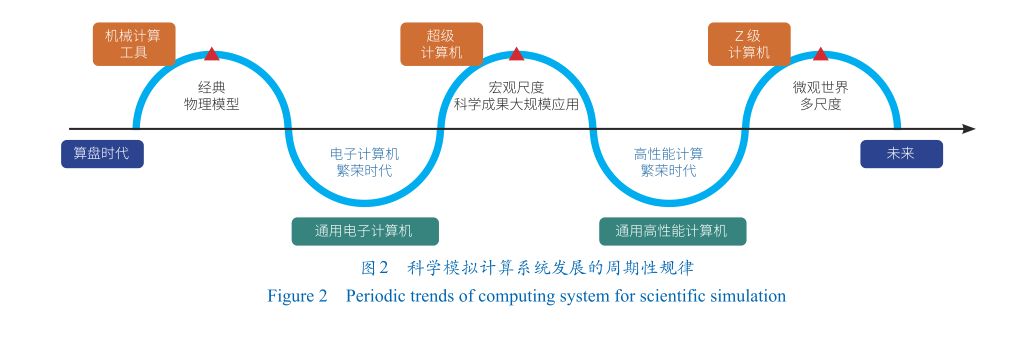
圖2 科學模擬計算系統發展的周期性規律
Figure 2 Periodic trends of computing system for scientific simulation
直觀上講,面向模擬智能的計算系統離不開智能組件(軟件和硬件),那么基于現有的智能組件來構建智能計算系統就能真正滿足模擬智能的需求嗎?答案是否定的。李國杰院士曾經指出:“有人曾戲謔目前信息領域的形勢為:‘軟件在吞噬世界,人工智能在吞噬軟件,深度學習在吞噬人工智能,GPU(圖形處理器)在吞噬深度學習。’”研究制造更高性能的GPU或類似的硬件加速器,似乎成了對付大數據的主要出路。但是如果不清楚該在什么地方加速,只盲目依靠硬件的蠻力是不明智的。因此,設計智能系統的關鍵在于深刻理解要求解的問題。計算機架構師的角色是選擇好的知識表示、識別開銷密集型任務、學習元知識、確定基本操作后,再用軟硬件優化技術去支持這些任務。”
面向模擬智能的計算系統設計是一個新產生的研究主題,相對其他計算系統設計而言,更加具有顯著的獨特性。因此,需要一個整體統一的視角,來推進人工智能和模擬科學的交叉。1989年,Wah和Li總結了關于智能計算機系統設計的3個層次,該觀點至今依然值得借鑒。但遺憾的是,目前還沒有任何關于這方面的更加深入的討論和實際性研究。具體而言,智能計算機系統的設計要考慮3個層次——表示層(representation level)、控制層(control level)和處理層(processor level)。表示層處理用于解決給定人工智能問題的知識和方法,以及如何表示該問題;控制層關注算法中依賴關系和并行性,以及問題的程序表示;處理層解決執行算法和程序表示所需的硬件和體系結構組件。下面將以這3個層次為基礎,討論面向模擬智能的計算系統設計的關鍵問題。
表示層
表示層是設計過程中的一個重要元素,包括領域知識表示和共性特征(元知識)表示,其決定了給定問題是否能夠在合理的時間內得到解決。定義表示層的本質是對適應廣泛應用的行為和方法進行高級抽象,將它們與特定的實現解耦。下面給出領域知識表示和共性特征表示的案例。
從現階段面向科學的人工智能研究看,對稱性的研究將成為表征學習的一個重要突破口,其原因在于物理上的守恒定律是由對稱性導致的(諾特定理),而守恒定律常被用來研究粒子的基本屬性和粒子之間的相互作用。物理上的對稱性是指在某種變換后或某種操作下的不變性,無法做出可辨別的測量(不可區分性)。基于多層感知機(MLP)、卷積神經網絡(CNN)、圖神經網絡(GNN)的小分子表征模型在有效加入對稱性之后,已經廣泛應用于蛋白質、分子、晶體等物質的結構預測。
2004年,Colella向美國國防高級研究計劃局(DARPA)提出了科學計算的“七個小矮人”(Seven Dwarfs)——稠密線性代數、稀疏線性代數、結構網格計算、非結構網格計算、譜方法、粒子方法、蒙特卡洛模擬。其中,每一種科學計算問題,都代表了一種可以捕獲計算和數據移動模式的計算方法。受此啟發,巴斯德實驗室的Lavin等以類似方式定義了模擬智能中的9種基元(nine motifs of simulation intelligence)——多物理現象多尺度建模、代理建模仿真、基于模擬的推理、因果關系建模推理、基于主體的建模、概率編程、微分編程、開放式優化、機器編程。這9種基元代表了互為補充的不同計算方法類型,為協同模擬和人工智能技術促進科學發展奠定了基礎。面向傳統科學計算歸納的各個主題,曾為應用于不同學科的數值方法(以及并行計算)的研發工作提供了明確的路線圖;面向模擬智能的各個主題同樣不局限于狹義的性能或程序代碼,而是激勵算法、編程語言、數據結構和硬件方面的創新。
控制層
控制層承上啟下,在整個計算系統中起到連接和控制算法映射與硬件執行的關鍵作用,在現代計算機系統中表現為系統軟件棧。本文僅討論和科學模擬相關的關鍵組件。模擬智能計算系統的控制層的變化主要來自2個方面:數值計算、大數據和人工智能的緊耦合;底層硬件技術可能發生的顛覆性變化。近年來,由于科學大數據的急劇增加,在科學模擬的數值計算階段,大數據軟件棧逐漸被超算系統領域所關注,只是相對于傳統的數值計算,大數據軟件棧是完全獨立的,在模擬流程上屬于不同的步驟。因此,基于2套系統的軟件棧是基本可行的。而在模擬智能階段,情況產生了根本上的變化。根據前文中所表示的問題解法描述公式y=F(f(x),A(x)),人工智能和大數據部分都是嵌入在數值計算內的,這種結合是一個緊耦合的模擬過程,自然需要一個異質融合的系統軟件棧。以DeePMD為例,該模型包含平移不變性的嵌入網絡、對稱性保持操作和擬合網絡3個模塊。鑒于體系的能量、受力等屬性不以人為定義改變(例如,便于測量或描述而賦予體系中各個原子的坐標),接入擬合網絡進行原子能量和受力的擬合,就能得到較高精度的擬合結果。再考慮模型的訓練數據強依賴于第一性原理計算,整個流程是一個數值計算和深度學習緊耦合的過程。
因此,系統軟件在代碼生成和運行時執行過程中,將不再區分共性核函數的來源,即不再區分是否由傳統人工智能、傳統數值計算或根據特定問題進行人工定制擴展得來。相應的,系統軟件一方面需要針對3類不同來源的共性核函數,提供易于擴展和開發的編程接口。另一方面則需要對這3類函數,在代碼編譯方面和運行時資源管理方面,兼顧并行效率和訪存局部性等性能保障;在面向不同粒度的計算任務時,能夠逐層進行融合和協同優化,發揮不同類型體系結構處理器的最佳性能。
處理層
縱觀數值計算階段到模擬智能階段,一個驅動技術發展的重要因素是當前硬件技術無法滿足計算需求。因此,處理層設計首要問題是:表示層的變化(如對稱性、基元)會產生全新的硬件體系架構嗎?它們是基于傳統專用集成電路(ASIC)實現,還是超越互補金屬氧化物半導體(CMOS)——從高性能計算的發展路線圖來看,這也是未來Z級超算的硬件設計要考慮的核心問題。可以大膽預測,在2035年左右,Z級超算可能會出現。盡管基于性能和可靠性因素的考慮,那時CMOS平臺仍將占據主流,但一些核心組件將是建立在非CMOS工藝上的專用硬件。
摩爾定律雖然放緩但依然有效,要重點解決的關鍵難題是如何逼近摩爾定律的極限。換句話說,如何通過軟硬件協同設計的手段,將基于CMOS的硬件潛力充分挖掘出來。因為,即使在性能優先級最高的超算領域,多數算法負載所獲得的實際性能僅僅只是硬件裸性能的極小部分。回顧超算領域早期發展階段,其基本設計哲學就是軟硬件協同。未來十幾年,微處理器迅速發展的“紅利”將耗盡,面向模擬智能的計算系統硬件架構應該回歸到從頭設計的軟硬件協同技術上。一個突出的例子是如前所述的分子動力學模擬,Anton系列是一個從零開始設計的超級計算機家族,可以滿足大規模長時間尺度的分子動力學模擬計算,而這也恰恰是對微觀世界探索的必要條件之一。然而,最新的Anton計算也只能對基于經典力場模型實現20微秒的模擬,無法進行第一性原理精度的長時間尺度模擬;然而,后者才能滿足多數實際應用(如藥物設計等)需求。
最近,作為模擬智能的典型應用,DeePMD模型在傳統大規模并行系統上的突破證明了其巨大的潛力。中國科學院計算技術研究所超算團隊,已實現了170個原子的第一性原理精度分子動力學的納秒級模擬。但是,長時間尺度模擬要求硬件架構具有極高的可擴展性,需要在運算邏輯和通信操作上有極致的創新。本文認為有2類技術可以預期能夠發揮關鍵作用:存算一體架構,通過降低數據移動的延遲來提高運算效率;硅光互連技術,可以在高能效下提供大帶寬的通信能力,有助于提高并行性和數據規模。進而,隨著對模擬智能應用廣泛而深入的研究,相信未來將逐步形成科學模擬領域的“新浮點”運算單元和指令集。
本文認為,在科學模擬的現階段,尚處于模擬智能階段的早期,此時對模擬智能的使能技術展開研究至關重要。在一般科學研究中,獨立的概念、關系和行為可能是易理解的。但是,它們的組合行為會導致不可預測的結果。深入了解復雜系統的動態行為,對于許多處理復雜挑戰性領域的研究人員來說是非常寶貴的。在面向模擬智能的計算系統設計中,一個必不可少的環節是跨學科合作,即領域科學、數學、計算機科學與工程、建模與仿真等學科工作者之間的協作。這種跨學科合作會構建更優的模擬計算系統,形成更全面和整體的方法,去解決更加復雜的現實世界的科學挑戰。
(作者:譚光明、賈偉樂、王展、元國軍、邵恩、孫凝暉,中國科學院計算技術研究所;編審:金婷;《中國科學院院刊》供稿)












