中國網(wǎng)/中國發(fā)展門戶網(wǎng)訊 計算概念具有豐富的內(nèi)涵，但由于概念體系不完善導(dǎo)致的名實之間的矛盾，在日常交流中計算概念內(nèi)涵的豐富性往往不能被準(zhǔn)確全面地反映。計算概念看似簡單，實則不然。計算不只是指加減乘除；進(jìn)一步說，計算也不只是指數(shù)值計算；更進(jìn)一步說，計算也不僅僅是指數(shù)學(xué)。究竟什么是計算，計算概念具有哪些方面，這些方面之間具有怎樣的關(guān)系，這些問題似乎比較基本，但答案并非顯而易見。計算概念包括數(shù)學(xué)理論、機(jī)械裝置、電氣裝置等方面，具有計算理論、計算技術(shù)、計算機(jī)器等不同內(nèi)容，涉及中國古代數(shù)學(xué)的算法、西方數(shù)學(xué)的形式推理等。準(zhǔn)確理解計算概念，需要涉及包括數(shù)學(xué)、物理學(xué)在內(nèi)的整個科學(xué)體系的深層次的核心內(nèi)容，需要正確把握科學(xué)與藝術(shù)、機(jī)械與巧思、幾何與代數(shù)、人腦與電腦、人類智能與人工智能、工藝基礎(chǔ)與上層建筑、證明與計算、功能與性能等一系列范疇對之間的關(guān)系。

計算概念因為計算技術(shù)本身具有深刻、普遍的影響力而在社會生活和科學(xué)研究中被高頻使用，因此計算概念的準(zhǔn)確性、完備性十分重要，但目前仍存在較多問題：算力和算法是經(jīng)常被使用的概念，但實際上算力本身的定義不清晰——算力是指計算機(jī)系統(tǒng)峰值計算能力，還是某個應(yīng)用的計算能力？假如是指計算機(jī)系統(tǒng)峰值計算能力，那么是指哪一指令類型的計算能力？算力是否受算法的影響？算術(shù)和算法的聯(lián)系和區(qū)別是什么？相對經(jīng)典計算來說，量子計算提升了計算的哪個方面？如何以統(tǒng)一的視角看待經(jīng)典計算和量子計算？在計算概念中，如何體現(xiàn)作為計算機(jī)系統(tǒng)設(shè)計者的人的作用？諸如此類的問題很重要，但使用目前的計算概念很難清楚地回答，原因除了應(yīng)用程序千變?nèi)f化、計算機(jī)指令集中指令類型豐富多樣、計算能力是關(guān)于多個因素的多元函數(shù)等客觀因素，還包括計算概念體系尚不完善。長期以來，我們對西方主導(dǎo)的計算概念采取了“拿來主義”的做法，并沒有及時對現(xiàn)有計算概念進(jìn)行審視、梳理、重構(gòu)和補(bǔ)遺。本文將吸收、借鑒和應(yīng)用我國古代思想，基于中國傳統(tǒng)思想文化對計算概念進(jìn)行對應(yīng)與分類，提出計算概念譜系。 

自主計算技術(shù)的重要性

計算機(jī)作為一種重要的生產(chǎn)工具，是第?3?次科技革命的重要代表，對社會發(fā)展具有極大的影響力。生產(chǎn)力是人類社會發(fā)展的最根本的決定性因素，生產(chǎn)工具是生產(chǎn)力發(fā)展水平的標(biāo)志。地球的歷史約?45?億年，人類的歷史約幾百萬年，文字的歷史約幾千年，而代表現(xiàn)代計算的計算機(jī)歷史僅有?70?多年，所以現(xiàn)代計算的歷史是短暫的；但是，計算技術(shù)在這短暫的時間內(nèi)產(chǎn)生的影響力是巨大的，計算技術(shù)代表的人類文明的高度是空前的。在本文中，我們將會看到我國第一屆國家自然科學(xué)獎一等獎的?3?位得主（錢學(xué)森、華羅庚、吳文俊）都對計算發(fā)表了自己的真知灼見，都分別作出了卓越貢獻(xiàn)。錢學(xué)森在?1957?年論述了如何構(gòu)思算法，華羅庚在?1956?年主持籌備創(chuàng)建了中國科學(xué)院計算技術(shù)研究所，吳文俊在?1976?年發(fā)現(xiàn)幾何定理的機(jī)械化證明方法，3?位大師的重視無疑體現(xiàn)出計算的重要性。

我國計算技術(shù)領(lǐng)域工作者長期致力于自主掌握最先進(jìn)的計算技術(shù)。世界上第一臺存儲程序式通用電子計算機(jī)（EDVAC）于?1946?年在美國賓夕法尼亞大學(xué)由馮?·?諾伊曼等人研制。作為“四項緊急措施”之一，中國科學(xué)院計算技術(shù)研究所于?1956?年成立，并于?1958?年研制出中國第?1?臺數(shù)字電子計算機(jī)。我國計算機(jī)在肇始階段，由于工業(yè)基礎(chǔ)薄弱，面臨缺少技術(shù)資料、電子器件、人才儲備的困境，而且整個軟硬件體系和生態(tài)也都需要從零建構(gòu)。盡管如此，我國計算機(jī)在總體設(shè)計、邏輯設(shè)計、工程設(shè)計和可靠性設(shè)計中仍然做到了較大的自主性。在體系建構(gòu)之后，我國國產(chǎn)計算機(jī)研發(fā)過程中經(jīng)歷了體制變革、西方壓制等內(nèi)外部挑戰(zhàn)，進(jìn)入時有曲折的發(fā)展軌道。國產(chǎn)計算機(jī)從?1960?年運算速度?150?次每秒，到?1973?年達(dá)到了?100?萬次每秒，再是?2008?年達(dá)到?100?萬億次每秒，現(xiàn)在已超過?10?億億次每秒。

在芯片、核心軟件等成為“卡脖子”技術(shù)的時代背景下，我國在計算技術(shù)領(lǐng)域需要建立一種理性、堅定、辯證、實用的文化自信。這種自信建立在事實考證和真理論證基礎(chǔ)上：不是盲目的，而是理性的、實事求是的；不是徘徊動搖的，而是堅定不移的；不是極端的，而是辯證的；不是空洞無用的，而是切實有用的。這種自信不僅僅是一種心理狀態(tài)，還是一種影響科學(xué)研究目的與路徑的思維和方法，關(guān)系到回答“為什么做研究”“做什么樣的研究”“怎樣做研究”等基本問題。中國當(dāng)代學(xué)生從小學(xué)到大學(xué)的數(shù)學(xué)學(xué)習(xí)主要以西方數(shù)學(xué)內(nèi)容為主，包括歐幾里得創(chuàng)立的公理化幾何學(xué)、牛頓-萊布尼茨創(chuàng)立的微積分等。對于中國古代的數(shù)學(xué)內(nèi)容及其蘊(yùn)含的思想文化，中國當(dāng)代學(xué)生則繼承較少。我們需要深化中華文明探源工程，夯實理性且堅定的文化自信的史實基礎(chǔ)。我國近代科技發(fā)展滯后，在新中國建立之后，我們用了較短的時間建立了基本完整的工業(yè)體系；在改革開放后，我們在全球化背景下、在科教興國戰(zhàn)略的指引下快速地實現(xiàn)了信息化。現(xiàn)階段我國在信息技術(shù)領(lǐng)域的部分細(xì)分方向受制于人，部分細(xì)分方向進(jìn)入“無人區(qū)”，進(jìn)一步的長足發(fā)展需要我們具有自主創(chuàng)新的勇氣和決心，進(jìn)而需要我們在厘清文化自信的史實的基礎(chǔ)上批判繼承和整理利用我國古代先進(jìn)深刻的思想。 

計算概念譜系化的意義

計算概念體系的完備性及準(zhǔn)確性，在文化發(fā)展和社會交流中具有重要作用。語言是思維的外殼，概念的缺位或粗糙，影響思維的表達(dá)。東西方有著不同的歷史文化特點，發(fā)展進(jìn)程不完全同步，在計算技術(shù)領(lǐng)域也是如此。清末數(shù)學(xué)家李善蘭在翻譯西方著作時，首創(chuàng)在漢語中原來并不存在的“微分”“積分”“函數(shù)”等名詞。物理學(xué)家胡剛復(fù)教授于?1923?年將來中國訪問的普朗克所說的“Entropy”翻譯為“熵”，這個字在漢語中之前并不存在。計算機(jī)科學(xué)家夏培肅院士是中文“位”（bit）、“存”（memory）的首次翻譯者。諸如此類的概念創(chuàng)新，為漢語世界引入了高頻使用的新元素，都具有重要開創(chuàng)意義。如果在漢語中沒有這樣的概念，或者即使有但不準(zhǔn)確，那么很多與這些概念相關(guān)的科學(xué)研究和文化交流活動將難以像今天這樣在中國正常進(jìn)行。計算概念譜系化，就是建立計算概念的“光譜”，即將原來籠統(tǒng)的計算概念解剖為多個子概念，這些子概念均有客觀存在的對應(yīng)物，而且這些對應(yīng)物之間的區(qū)分與轉(zhuǎn)化十分重要，也正因為這樣，譜系化就顯得十分必要。

中國古代數(shù)學(xué)和西方數(shù)學(xué)代表著計算技術(shù)的兩個方向、兩種風(fēng)格。中國古代數(shù)學(xué)達(dá)到較高的水平，風(fēng)格與西方不同。中國古代數(shù)學(xué)是以問題集的形式出現(xiàn)的，以《九章算術(shù)》為代表；其本質(zhì)是給出算法，注重實用性、具體性。古希臘數(shù)學(xué)以第一性原理（First Principles）的形式呈現(xiàn)，以《幾何原本》為代表；其本質(zhì)是證明，注重一般性、抽象性。對比《九章算術(shù)》和《幾何原本》，可發(fā)現(xiàn)前者具體、實用、直白，與實際生活結(jié)合緊密；后者抽象、系統(tǒng)、深刻，注重在前件與后件之間建立緊密的邏輯鏈條。實用通常是優(yōu)點，因為能立竿見影解決實際問題。但由于過度追求實用而導(dǎo)致放棄研究一般性、抽象性、非功利性問題的時候，實用就演變?yōu)閷嵱弥髁x，優(yōu)點變?yōu)槿秉c。因為這是一種基于趨利的“偷懶”和短視，是一種對自我認(rèn)知解放機(jī)遇的放棄。

中國需要自主的計算概念體系。目前，正處于?21?世紀(jì)第?3?個?10?年的開端，世界面臨百年未有之大變局，我們需要更加堅定不移地堅持文化自信。計算技術(shù)是文化的重要組成部分。隨著改革進(jìn)入深水區(qū)，與之前長期處于的“跟跑”狀態(tài)不同，我國在計算領(lǐng)域的更多方向?qū)⑻幱凇安⑴堋被颉邦I(lǐng)跑”狀態(tài)，有必要將“計算”這樣的重要概念中國化，繼而將中國的計算概念世界化，培育面向世界的具有中國特色的計算文化，以彰顯中國傳統(tǒng)文化精華的真理性和卓越性，從而更好地將重要概念沉淀到民族的文化基因中，更好地促進(jìn)原始創(chuàng)新。 

計算概念的譜系

中國古代數(shù)學(xué)為算法設(shè)計提供了示范。《九章算術(shù)》具有很高的實用性，其中給出了田地面積的計算方法“方田術(shù)”、糧食交易或兌換的計算方法“粟米術(shù)”、按比例分配的計算方法“衰分術(shù)”、由面積或體積求邊長的計算方法“少廣術(shù)”、土石工程中各種立體圖形體積的計算方法“商功術(shù)”、攤派賦稅徭役的計算方法“均輸術(shù)”、盈虧問題的計算方法“盈不足術(shù)”、線性方程組的求解方法“方程術(shù)”、直角三角形三邊互求的計算方法“勾股術(shù)”等實際問題的算法。雖然沒有公理化、形式化，但其真理性、原創(chuàng)性毋庸置疑。例如，其第九章提到，“勾股術(shù)曰：勾股各自乘，并，而開方除之，即弦。又股自乘，以減弦自乘，其余開方除之，即勾。又勾自乘，以減弦自乘，其余開方除之，即股”。這是勾股定理的完整表述，符號化并翻譯成現(xiàn)代漢語即為：設(shè)直角三角形三邊分別是?a、b、c，其中?a、b?為直角邊（勾、股），c?為斜邊（弦），則?c=√a2+b2，a=√a2—b2，b=√c2—a2。顯然，這里考慮了一般情況，公式對所有的直角三角形均成立。在西方，畢達(dá)哥拉斯、歐幾里得等僅求得了這個公式的幾種特殊情況，直到公元?3?世紀(jì)，丟番圖才取得相近結(jié)果。

我國古代曾經(jīng)產(chǎn)生的深刻哲學(xué)思想和技術(shù)思想，可被用于審視當(dāng)代的計算技術(shù)現(xiàn)狀，推動完善計算概念體系。例如，祖沖之在公元?5?世紀(jì)將圓周率估算到小數(shù)點后?7?位，直到?16?世紀(jì)，阿拉伯?dāng)?shù)學(xué)家阿爾?·?卡西才打破這一紀(jì)錄；西周數(shù)學(xué)家商高在公元前?11?世紀(jì)提出了勾股定理，早于希臘數(shù)學(xué)家畢達(dá)哥拉斯?500?多年。萊布尼茨創(chuàng)立了二進(jìn)位制，他于?1703?年在法國《皇家科學(xué)院院刊》發(fā)表的《論只使用符號?0?和?1?的二進(jìn)制算術(shù)兼論其用途及它賦予伏羲所使用的古老圖形的意義》中，確認(rèn)中國人在?3?000?年前的《易經(jīng)》六十四卦里就藏匿了二進(jìn)位制的奧秘。這些史實說明中國古代曾在數(shù)學(xué)和自然科學(xué)領(lǐng)域有重要發(fā)現(xiàn)或創(chuàng)造，也提示中國傳統(tǒng)文化中有許多值得挖掘的重要思想或方法，中華文明探源工程具有重要意義。

我國古代的哲學(xué)思想有助于我們深入理解計算概念的內(nèi)涵、重新梳理建立計算概念的體系。社會的運行與治理的過程，本身類似于計算的過程，具有并發(fā)、秩序等屬性，因此古代先賢的社會思想有可能被借鑒于計算技術(shù)領(lǐng)域。馮友蘭在《中國哲學(xué)簡史》中對中國古代哲學(xué)思想進(jìn)行了系統(tǒng)的歸納梳理，其中在第?14?章有這樣的總括性表述：“西周封建社會根據(jù)兩條原則辦事，一條是‘禮’，一條是‘刑’。禮是不成文法典，以褒貶來控制‘君子’即貴族的行為。刑則不然，它只適用于‘庶人’，即平民。所以《禮記》中說的：‘禮不下庶人，刑不上大夫。’”這里實現(xiàn)了二分類，其中“刑”是法家的研究對象，又可以一分為三；馮友蘭進(jìn)而指出，“韓非是法家最后的也是最大的理論家，在他之前，法家已經(jīng)有三派，各有自己的思想路線。一派以慎到為首，慎到與孟子同時，他以‘勢’為政治和治術(shù)的最重要的因素；一派以申不害為首，強(qiáng)調(diào)‘術(shù)’是最重要的因素；一派以商鞅為首，最重視‘法’。‘勢’指權(quán)力、權(quán)威，‘法’指法律、法制，‘術(shù)’指辦事、用人的方法和藝術(shù)，也就是政治手腕”。韓非認(rèn)為，“這三者都是不可缺少的”。

與上述歷史思想相對應(yīng)（表?1），計算概念可以細(xì)分為多個組分，分別是算勢（computational potential）、算力（computational power）、算術(shù)（computational arithmetic）、算法（computational algorithm）、算禮（computational ritual），它們構(gòu)成了計算概念的譜系。通過這個譜系，能夠深刻地、全面地理解和把握計算概念內(nèi)涵本身所具有的各個方面及其相互關(guān)系。這?5?個組分中，算禮具有鮮明的中國文化特點，算勢與算力做了區(qū)分，算法與算術(shù)做了區(qū)分；這些區(qū)分能夠清晰地反映計算技術(shù)領(lǐng)域的痛點，有助于討論解決這些痛點對應(yīng)的挑戰(zhàn)性問題。

算勢

算勢是某種理想狀態(tài)或條件下最大的潛在計算能力，不同數(shù)量級的算勢所能求解的問題復(fù)雜度也有數(shù)量級的差異。作為法家“勢”派的代表，“慎子曰：飛龍乘云，騰蛇游霧，云罷霧霽，而龍蛇與蚓蟻同矣，則失其所乘也”。意思是，法家“勢”派的代表人物慎到說：飛龍乘云飛行，騰蛇乘霧游動，然而一旦云開霧散，它們未免就跟蚯蚓、螞蟻一樣了，因為它們失去了騰空飛行的憑借。待求解問題與計算能力之間的關(guān)系，就像飛龍與云彩之間的關(guān)系一樣。

算勢是社會生產(chǎn)力的一個重要指標(biāo)，足夠的算勢是應(yīng)用程序或計算任務(wù)能夠運行的基礎(chǔ)。據(jù)《2020?全球計算力指數(shù)評估報告》顯示，計算力指數(shù)平均每提高?1?個百分點，數(shù)字經(jīng)濟(jì)和國內(nèi)生產(chǎn)總值（GDP）將分別增長?0.33%?和?0.18%。2016?年，谷歌旗下?DeepMind?公司研發(fā)的人工智能機(jī)器人阿爾法圍棋（AlphaGo）橫空出世，擊敗了世界著名圍棋棋手李世石，技驚四座。但不能忽視的是，訓(xùn)練?AlphaGo?花費了約?3?500?萬美元的計算資源。2018?年，谷歌提出?3?億參數(shù)的雙向語言表征模型（BERT），將自然語言處理推向了一個前所未有的新高度，但仍然是以足夠的計算能力作為基礎(chǔ)。

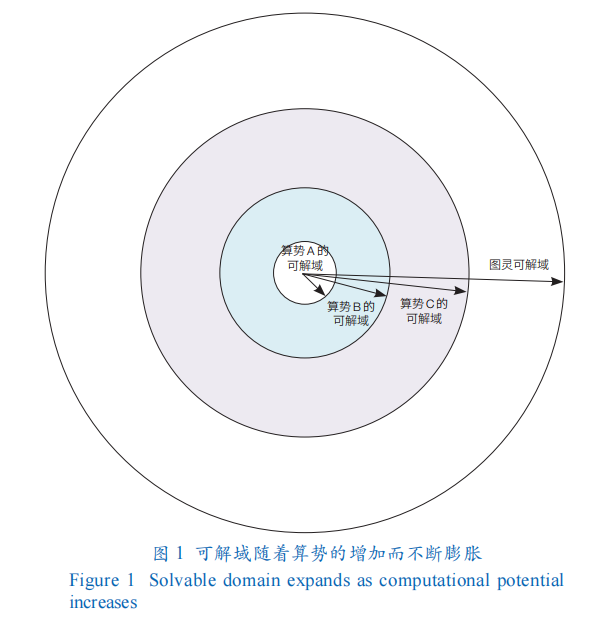
每一個量級的算勢對應(yīng)一個可求解的問題域（以下簡稱“可解域”）；隨著算勢增大，可解域也在增大（圖?1）。對于算勢?A?和算勢?B，它們對應(yīng)的可解域分別是?QA?和?QB?，若?A<B，則（QB—QA）所包括的是算勢?B?能夠求解而算勢?A?不能夠求解的問題。（QB—QA）體現(xiàn)了算勢增加對求解某些問題所具有的不可替代的使能作用。算勢的單位是隨應(yīng)用程序而變化的。例如：對浮點操作密集型應(yīng)用程序來說，算勢的單位是“浮點操作數(shù)每秒”（FLOPS）；對于事務(wù)處理密集型應(yīng)用程序來說，算勢的單位是“事務(wù)數(shù)每秒”（TPS）。

算勢是因時因地而變的——每個時代有自己的算勢，每個國家或地區(qū)有自己的算勢。2022?年我國提出并開始實施“東數(shù)西算”工程，該工程與“西氣東輸”“西電東送”“南水北調(diào)”等一樣都是資源跨域調(diào)配戰(zhàn)略工程。針對我國東、西部算勢分布總體呈現(xiàn)出“東部不足、西部過剩”的不平衡局面，引導(dǎo)中西部利用能源優(yōu)勢建設(shè)計算基礎(chǔ)設(shè)施——“數(shù)據(jù)向西，算力向東”，服務(wù)東部沿海等算力緊缺區(qū)域，以解決我國東西部算勢分布不均衡、供需不平衡的問題。

算勢的概念可以促進(jìn)我們理解經(jīng)典串行計算、經(jīng)典并行計算、量子計算之間的聯(lián)系和區(qū)別：經(jīng)典并行計算（或超級計算）相對于串行計算，是為了增加算勢；量子計算相對于經(jīng)典計算，也是為了增加算勢。夏培肅院士畢生后投身于研制高性能經(jīng)典計算機(jī)的實踐，她的丈夫楊立銘院士畢生從事理論物理的研究，先后培養(yǎng)了曾瑾言、錢伯初等量子力學(xué)教育家。他們無論是做工程實踐，還是做理論研究，無論是做經(jīng)典計算機(jī)，還是做量子計算機(jī)，從根本上說都是為了增加算勢。需要指出，一方面，經(jīng)典并行計算、量子計算能極大地提高算勢；另一方面，1936?年圖靈研究判定性問題時所提出的圖靈機(jī)模型是串行的。但經(jīng)典并行計算、量子計算不會改變問題的不可求解性；也就是說，如果一個問題在串行圖靈機(jī)上是不可求解的，那么通過經(jīng)典并行計算、量子計算仍然不可解（圖?1）。

算力

算力是應(yīng)用程序所能實際獲得的計算能力，其上界是算勢，來源于算勢，受限于算勢，但不等同于算勢；如何彌合兩者之間的鴻溝，實現(xiàn)從算勢到算力的高效轉(zhuǎn)化，是包括計算機(jī)系統(tǒng)結(jié)構(gòu)和系統(tǒng)軟件在內(nèi)的整個計算機(jī)學(xué)科需要研究解決的核心問題。算勢轉(zhuǎn)化為算力的過程依賴很多條件或因素，如應(yīng)用程序的特征、運行環(huán)境的特征、多處理器之間負(fù)載是否均衡等。一方面，要注意算勢的基本限制作用，盡量提高算勢；另一方面，要注意算勢向算力的充分轉(zhuǎn)化，盡量充分利用算勢。這?2?個方面目標(biāo)一致，不可偏廢。

各種類型的計算機(jī)都存在算勢向算力轉(zhuǎn)化不充分的問題（表?2）。例如，在超級計算機(jī)上，普通用戶的很多程序往往效率較低。2022?年圖靈獎得主杰克·唐加拉參與編制的線性系統(tǒng)軟件包（LINPACK）成為評測超級計算機(jī)的工具，但該工具只代表較為理想的情況，因為其中包含良好的局部性、易開發(fā)的并行性特點的大量稠密矩陣計算。基準(zhǔn)測試程序（HPCG）則代表了大量實際應(yīng)用中常出現(xiàn)的不易擴(kuò)展和開發(fā)局部性的稀疏計算和訪存模式。測試基準(zhǔn)?Graph500?代表了數(shù)據(jù)密集型應(yīng)用的情況。戈登?·?貝爾（Gordon Bell）獎應(yīng)用則代表了算法優(yōu)化所能帶來的效率提升。

算術(shù)

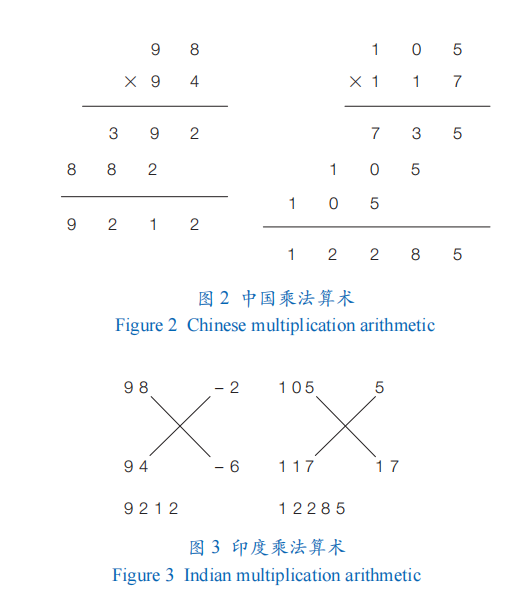
算術(shù)是關(guān)于數(shù)值的算法，是狹義的算法，也是最基本、最顧名思義的算法。算術(shù)強(qiáng)調(diào)四則運算、開方、乘方等計算的技巧。例如，馮?·?諾伊曼在?1945?年的?EDVAC?研制報告中就用了多個章節(jié)分別討論了這些方面，以及中國乘法和印度乘法就使用了不同的技巧。以?2?位數(shù)和?3?位數(shù)乘法為例，中國乘法建立在逐位相乘的基礎(chǔ)上（圖?2）；印度乘法建立在求差值的基礎(chǔ)上，將對角線上的數(shù)字之和作為結(jié)果的高位，將差值的乘積作為結(jié)果的低位（圖?3）。從中可以直觀地感受到中國乘法和印度乘法使用了不同的技巧。

算法

算法是廣義的計算方法，包括數(shù)值算法、非數(shù)值算法，強(qiáng)調(diào)計算的機(jī)械的規(guī)則。吳文俊等創(chuàng)立和發(fā)展了數(shù)學(xué)機(jī)械化。只有機(jī)械化，才能由計算機(jī)自動去執(zhí)行。幾何定理的證明分為?2?個步驟：①幾何的代數(shù)化與坐標(biāo)化。從幾何的公理系統(tǒng)出發(fā)，引進(jìn)數(shù)系統(tǒng)與坐標(biāo)系統(tǒng)，使得任意幾何定理的證明問題成為代數(shù)問題。②幾何的機(jī)械化。將幾何定理假設(shè)部分的代數(shù)關(guān)系式進(jìn)行整理，然后按照確定步驟（編寫為程序）驗證定理終結(jié)部分的代數(shù)關(guān)系式是否可以從假設(shè)部分已整理成序的代數(shù)關(guān)系式推出。

盡管算法是由人腦設(shè)計，但人腦本身不善于執(zhí)行機(jī)械的規(guī)則；同時，大量的問題往往通過機(jī)械的規(guī)則（即通過算法而不是巧思）更容易解決。人腦善于巧思，但不善于反復(fù)枯燥的操作，這可能與人腦本身所具有的多巴胺等物質(zhì)比較稀缺，以及獨特的獎勵懲罰機(jī)制有關(guān)。以幾何為例來說明，幾何分為綜合幾何和解析幾何。綜合幾何就是我國初中所教授的幾何，其解題往往需要觀察、“巧妙”地添加輔助線，也就是需要人腦的巧思。借助圖形的直觀形象，以一些基本名詞（如點、直線、平面等）和關(guān)系（如銜接、順序、相似等），滿足一套公理或公設(shè)，經(jīng)過一定的邏輯推理，導(dǎo)出一系列的定理的研究方法，被稱為古典公理法或綜合法，而用這種方法所研究的幾何被稱為綜合幾何。綜合幾何與?17?世紀(jì)笛卡爾創(chuàng)立的解析幾何相對。吳文俊指出，綜合幾何盡管直觀生動，但使用范圍“頗為有限”，相反解析幾何應(yīng)用范圍很廣。

算法強(qiáng)調(diào)?2?個方面，且需要具備?5?個特征。2?個方面為：①功能——能否計算；②性能——能以多快的速度計算。5?個特征為：①有窮性（finiteness）——必須在有限的步驟內(nèi)終止；②確定性（definiteness）——每一步驟必須被精確地、嚴(yán)格地定義，不能有歧義性；③輸入（input）——有0個或多個輸入；④輸出（output）——至少有?1?個輸出；⑤能行性（effectiveness）——所涉及的操作必須足夠基本，以致操作在原理上能被人用鉛筆和紙在有限的時間內(nèi)完成。

以上?5?個特征之中的能行性涉及一個內(nèi)容深刻的重要學(xué)科方向——可計算性理論。可計算性理論是很多計算機(jī)從業(yè)者較為欠缺的。可計算性理論有很多結(jié)論是與沒有經(jīng)過這方面訓(xùn)練的人的直覺相反的，這樣的結(jié)論實例有：①可計算的本質(zhì)是遞歸；②算法的數(shù)量是可數(shù)的（而實數(shù)的數(shù)量是不可數(shù)的）；③不存在一般過程能夠在有限步內(nèi)判定一個計算過程是否是算法。一個給定的問題是否存在對應(yīng)的算法，是一個關(guān)于“是否可解”的問題。如果存在對應(yīng)的算法，怎樣找出或構(gòu)造出這個算法，是一個關(guān)于“如何求解”的問題；這往往涉及人類對于問題所處領(lǐng)域的理解，也就是通常所說的“know-how”，即技術(shù)訣竅、專業(yè)知識、私家配方（“秘方”）。

計算機(jī)、算法都是人腦設(shè)計的，人工智能歸根結(jié)底是人類智能的外化（externalization）和自動化（automation）。錢學(xué)森在?1957?年發(fā)表的《論技術(shù)科學(xué)》中闡述，“......技術(shù)科學(xué)工作中最主要的一點是對所研究問題的認(rèn)識。只有對一個問題認(rèn)識以后才能開始分析，才能開始計算。但是什么是對問題的認(rèn)識呢？這里包含確定問題的要點在哪里，什么是問題中現(xiàn)象的主要因素，什么是次要因素；哪些因素雖然也存在，可是它們對問題本身不起多大作用，因而這些因素就可以略而不計。要能做到這一步，我們必須首先做一些準(zhǔn)備工作，收集有關(guān)研究題目的資料，特別是實驗數(shù)據(jù)和現(xiàn)場觀察的數(shù)據(jù)，把這些資料印入腦中，記住它，為做下一階段工作的準(zhǔn)備，下一個階段就是真正創(chuàng)造性的工作了。創(chuàng)造的過程是：運用自然科學(xué)的規(guī)律為摸索道路的指南針，在資料的森林里，找出一個道路來。這條道路代表我們對所研究的問題的認(rèn)識，對現(xiàn)象機(jī)理的了解。也正如在密林中找道路一樣，道路決難順利地一找就找到，中間很可能要被不對頭的蹤跡所誤，引入迷途，常常要走回頭路......把問題認(rèn)識清楚以后，下一步就是建立模型......有了模型了，再下一步就是分析和計算了……”。

上面描述的就是人腦構(gòu)思或構(gòu)造算法的過程。算法的構(gòu)思或構(gòu)造處于人類認(rèn)識客觀世界的最前沿，算法離不開人腦所進(jìn)行的“創(chuàng)造性的工作”，實際上“希爾伯特計劃”失敗的原因就在于此，即判定性問題的答案是否定的；也就是說，不存在一般過程能夠在有限步內(nèi)判定一個計算過程是否是算法。

算禮

人腦與計算機(jī)之間存在著緊密聯(lián)系，又存在著內(nèi)在機(jī)制和語義溝通上的鴻溝。人腦具有與計算機(jī)不同的特點。相對計算機(jī)，人腦有直覺、大局觀，但不善于快速精確計算和記憶。計算機(jī)又稱電腦，是實現(xiàn)或執(zhí)行人工智能算法的載體；同時，人工智能算法又可以用來設(shè)計計算機(jī)，于是就出現(xiàn)了用電腦設(shè)計電腦的現(xiàn)象。但就根源來說，計算機(jī)、人工智能算法都是人腦的設(shè)計結(jié)果，而設(shè)計過程本質(zhì)上是計算。但是，對大多數(shù)研究和設(shè)計人員來說，計算機(jī)系統(tǒng)長期以來是一個“黑箱”，缺乏可分析的抽象，人腦很難精確、全面地分析。以深度學(xué)習(xí)為代表的很多人工智能算法存在一個長期以來為人詬病的弊端：人工智能算法是一個“黑箱”，可解釋性、透明性、可分析性不強(qiáng)。人腦設(shè)計的產(chǎn)物反而不能被人腦理解，這成為一個亟待破解的悖論。

算禮是關(guān)于計算如何在計算機(jī)系統(tǒng)上進(jìn)行的制度規(guī)范；其比算法更接近人腦這一端，更關(guān)注計算機(jī)系統(tǒng)的整體，強(qiáng)調(diào)計算的系統(tǒng)可被人腦直接進(jìn)行評估。算法是關(guān)于單一應(yīng)用內(nèi)部計算方法的說明，聚焦于應(yīng)用個體；算禮除了考慮每個算法之外，還考慮運行在同一系統(tǒng)之上的多個算法之間的協(xié)調(diào)有序，聚焦于系統(tǒng)整體。高通量計算、低熵數(shù)據(jù)中心都體現(xiàn)了這一點。高通量計算并不關(guān)注單個應(yīng)用或單個請求的性能，而是關(guān)注大批量高并發(fā)的應(yīng)用或請求的整體吞吐量；對個體應(yīng)用而言，其性能相比于理想時（即單獨運行時）一般變差了，但相對低通量時的排隊延遲導(dǎo)致的不可服務(wù)性來說，性能有了很大的提升。

算禮是不成文的，相對算法而言是軟性的，但其褒貶意義上的影響力不可替代。褒貶就是評估（evaluation），通過褒貶，社會系統(tǒng)之中多個主體之間的關(guān)系得到調(diào)節(jié)和規(guī)范，社會系統(tǒng)在很多發(fā)展可能之中篩選出符合禮的那一種。在西周時期，周王室與諸侯國之間“保持著社會的、外交的接觸，如果有什么事情要處理，也都遵循他們不成文的‘君子協(xié)定’。這就是說，他們是尊禮而行”。法的執(zhí)行往往需要較大的時間成本和資源成本，原型系統(tǒng)實現(xiàn)和基準(zhǔn)程序測試也往往需要較大的時間成本和資源成本。一方面，設(shè)計空間和應(yīng)用空間都極其龐大，進(jìn)而設(shè)計空間與應(yīng)用空間的笛卡爾積更加龐大；另一方面，原型系統(tǒng)實現(xiàn)和基準(zhǔn)程序測試的緩慢。兩者造成尖銳的矛盾，增大了實現(xiàn)應(yīng)用程序與系統(tǒng)結(jié)構(gòu)之間良好匹配的難度。因此，需要通過算禮，在原型系統(tǒng)實現(xiàn)和基準(zhǔn)程序測試之前，就能夠分析出該系統(tǒng)的主要性質(zhì)，進(jìn)而篩掉不合適的候選系統(tǒng)，大幅度提高設(shè)計敏捷度，加速人類智能向人工智能的轉(zhuǎn)化、外化、物化的過程。

算禮的必要性毋庸置疑，算禮的可行性需要加強(qiáng)研究。算禮要解決的是：不依賴機(jī)器條件下，如何開展計算機(jī)這樣的復(fù)雜系統(tǒng)的頂層設(shè)計。需要解決人腦思維所需要的元素的命名與抽象問題，要能反映計算機(jī)系統(tǒng)的實際狀況，又要便于人腦記憶與推理。諸如模型、分治、分層、模塊化、經(jīng)驗法則等思想或技術(shù)可以被運用此過程，以使能或加速人腦進(jìn)行系統(tǒng)頂層設(shè)計和敏捷開發(fā)。 

計算概念譜系組分的相互關(guān)系

計算概念譜系將計算概念的內(nèi)涵細(xì)分，形成一個立體的相互聯(lián)系的有機(jī)整體（圖?4）。算勢、算力、算術(shù)、算法、算禮是同一事物（計算）的不同方面，它們有著不同的側(cè)重點，又有著相同的目的或價值取向，即為了計算系統(tǒng)更快、更好地完成待求解的應(yīng)用問題。圖?4?是一個三角雙錐，算術(shù)、算法、算禮?3?個因素構(gòu)成一個三角形，本質(zhì)上是計算的映射面，其上部和下部各有一個頂點，下部頂點是算勢，上部頂點是算力，算勢向算力的轉(zhuǎn)化是計算的主線（映射線），計算的映射面的狀況決定了算勢向算力的轉(zhuǎn)化率。

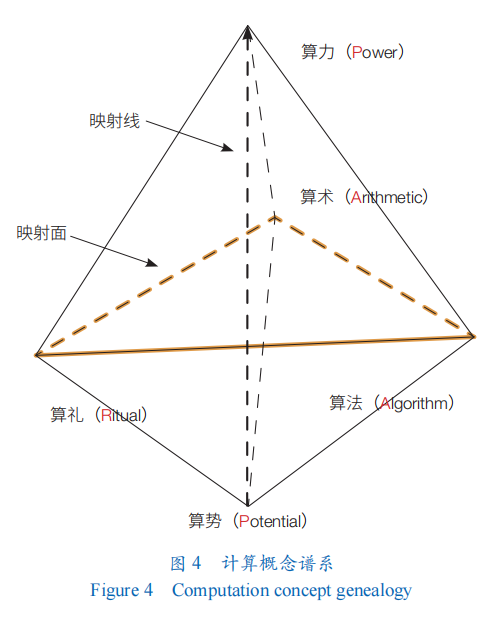
算禮是算法的前序，算法是算術(shù)的推廣，算勢是算力的基本限制。我們需要攻克高端光刻機(jī)技術(shù)，不斷地改進(jìn)工藝，擴(kuò)大算勢；同時，我們要通過跨層垂直優(yōu)化等技術(shù)提高算勢向算力的轉(zhuǎn)化率，在算勢不變或增加緩慢時，仍可獲得較高的算力。

算勢與算術(shù)、算法之間有著微妙的互補(bǔ)或替代關(guān)系。例如，當(dāng)算勢足夠大的時候，算勢的強(qiáng)大可以彌補(bǔ)算術(shù)的笨拙，所以此時算術(shù)或算法技巧的巧妙高明未必很重要，只起到錦上添花的作用；當(dāng)算勢不充分的時候，如由于芯片制造工藝被“卡脖子”或者由于東西部算勢不均衡，算術(shù)或算法性能優(yōu)越就非常必要，應(yīng)起到雪中送炭的作用。

人工智能來源于人，又最終服務(wù)于人，因此計算的內(nèi)涵在各個方面、環(huán)節(jié)之間的轉(zhuǎn)化率問題至關(guān)重要。算禮關(guān)注人類智能向人工智能的轉(zhuǎn)化、建立人腦與電腦之間的橋梁，算法關(guān)注輸入與輸出之間的轉(zhuǎn)化過程、建立已知與未知之間的橋梁，算禮與算法均提供轉(zhuǎn)化可能、提高轉(zhuǎn)化效率。算勢與算力之間有著不同程度的鴻溝，存在著轉(zhuǎn)化的問題。算力與滿足人類日益增長的美好生活需要之間也存在著鴻溝，也存在著轉(zhuǎn)化的問題。 

計算概念具有重要作用，需要我們建立清晰的譜系以彰顯其豐富的內(nèi)涵。計算概念的中國化是增強(qiáng)文化自信的重要步驟。堅定的自信需要建立在，也只能建立在對客觀史實、客觀真理的理性認(rèn)知基礎(chǔ)上。真理是無國界的，西方計算概念的中國化與中國計算概念的世界化同時發(fā)生、相向而行、相互補(bǔ)充。將中國傳統(tǒng)思想文化的優(yōu)秀部分與現(xiàn)代科技的重要概念無縫銜接起來，有助于發(fā)揚(yáng)和彰顯傳統(tǒng)文化的真理性，同時也有助于使用傳統(tǒng)文化詞匯來思考現(xiàn)代科技問題。中國古代基于時間長度、人口數(shù)量、文明高度，積累了巨大的歷史遺產(chǎn)；中國歷史上存在的數(shù)以億萬計的人腦（即祖先的大腦）計算或思索的成果形成了一個寶庫，在核心技術(shù)“卡脖子”、人口老齡化等國內(nèi)外危機(jī)疊加頻發(fā)的背景下，尤其值得并需要當(dāng)代人挖掘、整理和提高。

（作者：劉宇航、張菲，中國科學(xué)院計算技術(shù)研究所；《中國科學(xué)院院刊》供稿）

相關(guān)文章